首页 算法 动态规划

# DFS

搜索和 DP 不分家，几乎所有的 DP 都能用搜索解决（虽然复杂度可能较劣）。不过，如果实在想不出正解，DFS 不失为骗分的好手段。

主要的搜索算法有：

  1. DFS/BFS 爆搜
  2. 双向 BFS
  3. 启发式搜索（又称 A*）
  4. 迭代加深搜索
  5. IDA*（迭代加深 + 启发式）
  6. 记忆化搜索
  7. 剪枝

重要程度：1,7,6 > 4,3 > 5,2。

# P3956 [NOIP2017 普及组] 棋盘

搜索 / DP 的题一定要先看数据范围。这道题 1≤m≤100,1≤n≤10001 ≤ m ≤ 100, 1 ≤ n ≤ 1000，朴素搜索显然不可行。

然后分析题目，到达一个点可能有多种途径，所以也不可以用 vis 数组优化。只剩记忆化搜索了。

简单证明一下正确性：

  • 如果当前格子本来就有颜色，那么魔法一定可用
  • 如果当前格子原本没有颜色，那么只要搜到这个格子，魔法其实只有一种情况就是不可用

记搜时注意剪枝条件一定要写满。比如 f >= mem[x][y] 如果改成 f > mem[x][y] ，后果就会很严重。

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int m, n, c[N][N], mem[N][N];
int d[4][2] = <!--swig0-->;
int ans = 0x3f3f3f3f;
void dfs(int x, int y, int f, int cc) {
	
	//f: 代价
	//cc != -1 不能用魔法，此处改成的颜色
	//cc == -1 可以
	
	if(f >= mem[x][y] || f >= mem[m][m]) return;
	mem[x][y] = f;
	
	if(x == m && y == m) return;
	
	for(int i=0; i<4; ++i) {
		int xx=x+d[i][0],yy=y+d[i][1];
		if(xx<1||xx>m||yy<1||yy>m) continue;
		if(cc!=-1&&c[xx][yy]==cc||cc==-1&&c[xx][yy]==c[x][y]) {
			dfs(xx, yy, f, -1);			
		} else if(cc!=-1&&c[xx][yy]!=cc&&c[xx][yy]!=-1||cc==-1&&c[xx][yy]!=c[x][y]&&c[xx][yy]!=-1) {
			dfs(xx, yy, f+1, -1); 
		} else if(cc==-1&&c[xx][yy]==-1) {
			dfs(xx, yy, f+2, c[x][y]);
		}
	}
}
int main() {
	
	scanf("%d%d", &m, &n);
	
	memset(c, -1, sizeof c);
	memset(mem, 0x3f, sizeof mem);
	
	for(int i=1; i<=n; ++i) { 
		int x, y, cc; scanf("%d%d%d", &x, &y, &cc); 
		c[x][y] = cc;
	}
	
	dfs(1, 1, 0, -1);
	
	printf("%d\n", mem[m][m] == 0x3f3f3f3f ? -1 : mem[m][m]);
	return 0;
}
# P3959 [NOIP2017 提高组] 宝藏
可能你会想到生成树，所以这里给出一个反例：
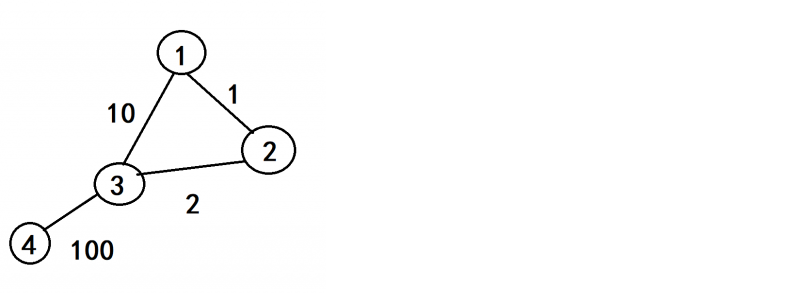
这张图从 1 号点开始的 Prim 便是错的。
如果跑 Prim，从 1 号点开始的话，我们会先访问 2，（此时花费为 1），然后我们会访问 3，此时花费为 3 * 2，然后由于只有 4 号点未访问，这时 3 号的访问顺序为 3，访问 4 号的代价是 3 * 100 = 300，显然这种做法不是最优的，正确的答案应该是 211（从 1 号点开始的最小花费为 211）。
虽然直接跑 Prim 是错的，但是 Prim 的思想仍然重要，这一思想也在最短路等很多算法中有应用：用更新过的点去更新其他点。
我们设计一个不基于点的 dfs 函数，参数只需传递代价，每次迭代，先枚举访问过的点，再枚举一个未访问且未开通路径的点，进行松弛，将代价持续传递下去。计算代价需要记录点的深度，也要通过父节点传递下去。
这样我们就有了一个大概的思路，照着模拟，可以拿到至少 70 分。
# Code:
#include <cstdio>
#include <cstring>
const int INF = 0x7f7f7f7f;
int min(int a, int b) { return a < b ? a : b; }
int map[20][20];
int dep[20], best, n, m, num;
bool vis[20];
void dfs(int x) {
	if(x >= best) return; // 注意这里的剪枝！
	if(num == 0) {
		best = x;
		return;
	}
	for(int i=1; i<=n; ++i) {
		if(vis[i]) {
			for(int j=1; j<=n; ++j) {
				if(!vis[j] and map[i][j] < INF) {
					vis[j] = true; --num;
					dep[j] = dep[i] + 1;
					dfs(x + map[i][j] * dep[j]);
					vis[j] = false; ++num;
				}
			}
		}
	}
}
int main() {
	memset(map, 0x7f, sizeof map);
	
	scanf("%d%d", &n, &m);
	
	for(int i=1; i<=m; ++i) {
		int x, y, v;
		scanf("%d%d%d", &x, &y, &v);
		map[x][y] = map[y][x] = min(map[x][y], v);
	}
	
	best = INF; num = n;
	for(int i=1; i<=n; ++i) {
		vis[i] = true; --num;
		dep[i] = 0;
		dfs(0);
		vis[i] = false; ++num;
	}
	
	printf("%d\n", best);
	
	return 0;
}
按当年的测试数据，在这段代码的基础上再进行足够细致的剪枝，可以拿到 100 分的好成绩。
# 状压 DP
# 常用操作
设全集为 xx
  • for(int y = x; y; y = (y-1) & x) ：枚举 x 的每个子集
  • x^y ：x 集合中刨去 y
  • x&y == y ：y 是 x 的子集
# P3959 宝藏
对还是刚才那道题。
即便当时的测试数据水到乱搞都可以打满，但是搞懂正解仍然很有必要。
设计状态，令 fj,i,Sf_{j,i,S} 表示从起点到准备向外发边的点 ii 的距离为 jj，准备要把集合 SS 中的点挖通。
转移时，枚举从节点 ii 打出的边 (i,k)(i,k)，再枚举从 kk 要打通的子集 S2⊂SS_2\subset S，那么
fj,i,S=min⁡k∈S2⊂S(d[i][k]∗(j+1)+fj+1,k,S2−{k}+fj,i,S−S2)f_{j, i, S} = \min_{k \in S_2 \subset S} (d[i][k] * (j + 1) + f_{j + 1, k, S_2 - \{k\}} + f_{j, i, S - S_2})
转移顺序一定要想好。
最后取所有 f0,i,U−if_{0,i,U-{i}} 的最小值即可，其中 UU 是全集。
核心代码
// 预处理集合中 1 的个数
    for (int i = 1; i < mx; ++i)
        sz[i] = sz[i & (i - 1)] + 1;
    // 预处理 lowbit
    for (int i = 0; i < n; ++i)
        mn[1 << i] = i;
    for (int i = 1; i < mx; ++i)
        mn[i] = mn[i & -i];
    for (int i = 0; i < n; ++i)
        f[n - 1][i][0] = 0; // 初值
    for (int j = n - 2; j >= 0; --j) { // 距离
        for (int i = 0; i < n; ++i) { // 发边点
            f[j][i][0] = 0; // 初值
            for (int S = 1; S < (1 << n); ++S) {
                if (((~S >> i) & 1) //i 不在集合 S 里
                        && sz[S] <= n - j - 1)  // 不会多挖
                    for (int S2 = S; S2; S2 = (S2 - 1) & S) { //S 的每个子集
                        int tmp = S2;
                        for (int k = mn[tmp]; tmp; k = mn[tmp &= ~(1 << k)]) //S2 里的每个点
                            if (mp[i][k] ^ INF) // 存在待挖的边
                                f[j][i][S] = min(f[j][i][S], f[j + 1][k][S2 & ~(1 << k)] + f[j][i][S & ~S2] + mp[i][k] * (j + 1));
                    }
            }
        }
    }
    int ans = INF;
    for (int i = 0; i < n; ++i)
        ans = std::min(ans, f[0][i][(mx - 1) & ~(1 << i)]);
     
 更新于