首页 算法 网络流

# 网络流：消圈算法

注：下文中的权均表示费用。

# 消圈定理

在某个流 ff 中，如果其残余网络中没有负圈（剩余流量为 00 的边视为不存在），那它一定是当前流量下的最小费用，否则一定不是。

# 证明

假设一个网络，所有边的容量都是 11。

img

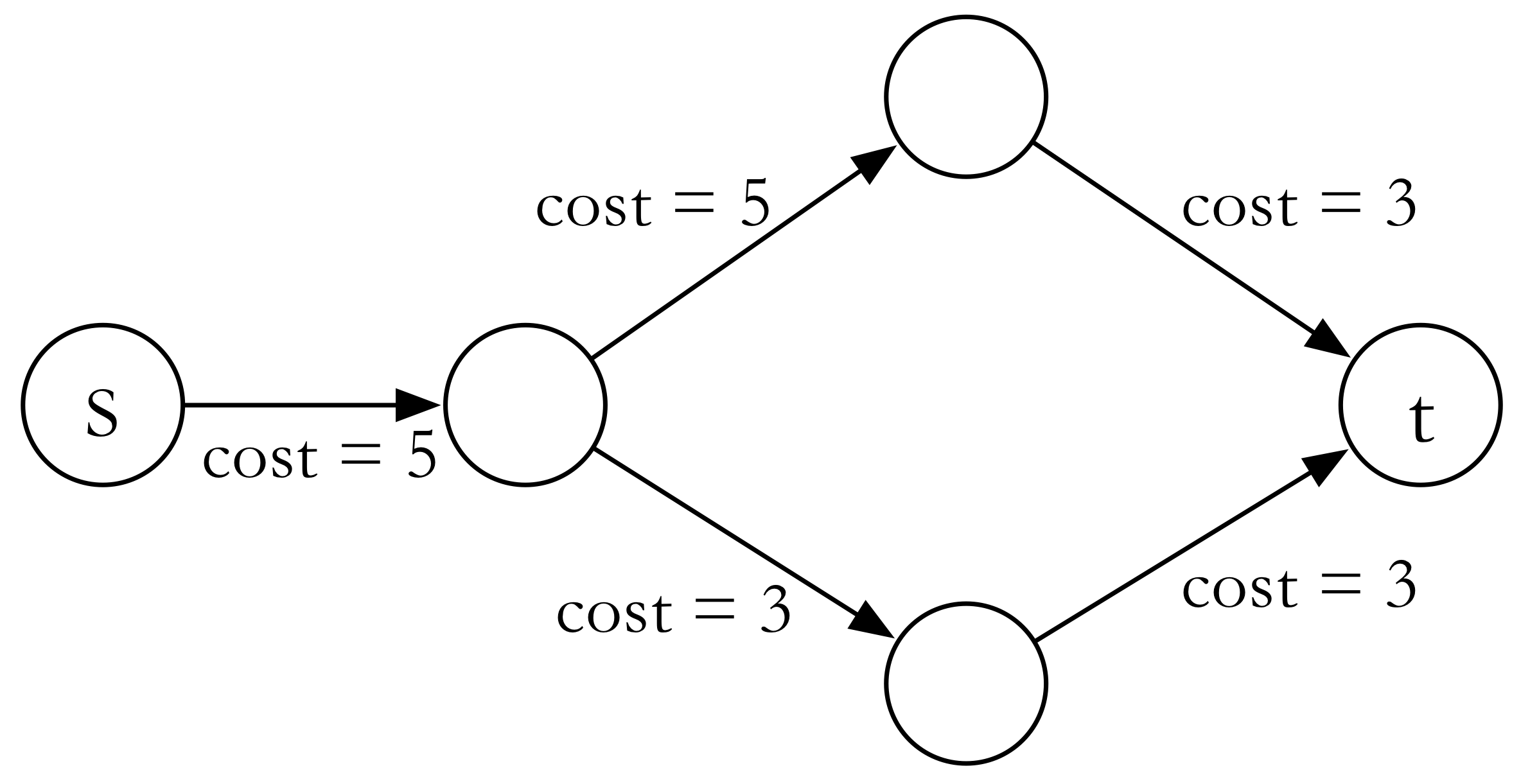
如果流量走上路的话，其残余网络（黑箭头）变为：

img

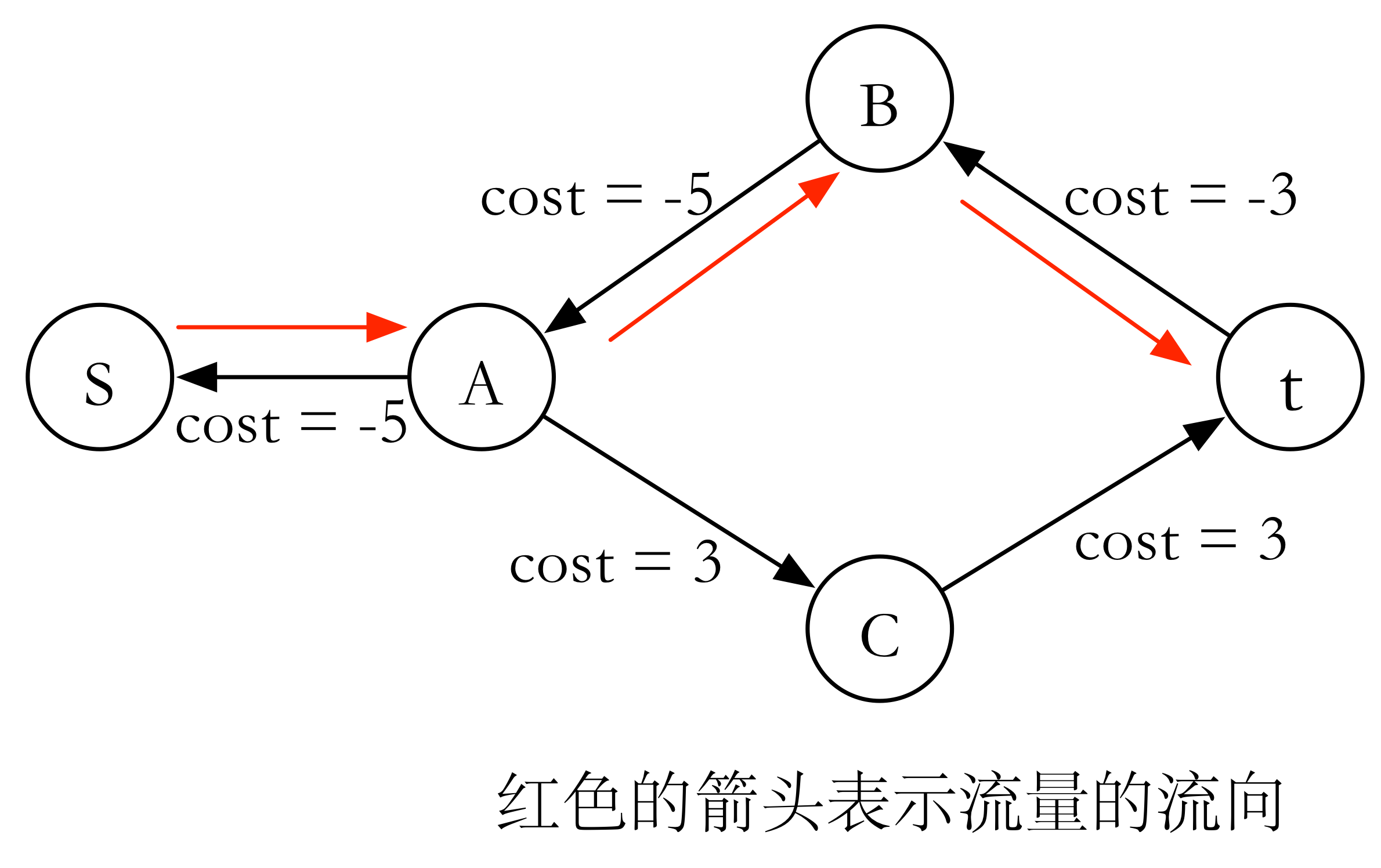
因为上路的边的流量占满了，所以现在上路只有反边。

显然 A→C→t→B→AA \rightarrow C \rightarrow t \rightarrow B \rightarrow A 为负圈，沿此负圈增广（每条边的流量＋1），环上每个点的入流量仍然等于出流量（原流为可行流）。

流量在圈中增广，总的流量既没有增加，也没有减少，只不过是流量从费用更少的地方流过 （A→C→tA \rightarrow C \rightarrow t），从费用大的地方退流而已（t→B→At \rightarrow B \rightarrow A），流过的流量和退掉的流量是相等的，实质上只是将从 AA 流出的流量的方向改变，使得费用更小。

网络流的反边给了我们一个很好的反悔机制，使得我们可以对任意一个流 ff，通过消负圈（可能不止一个），来得到它当前流量下的最小费用流。

img

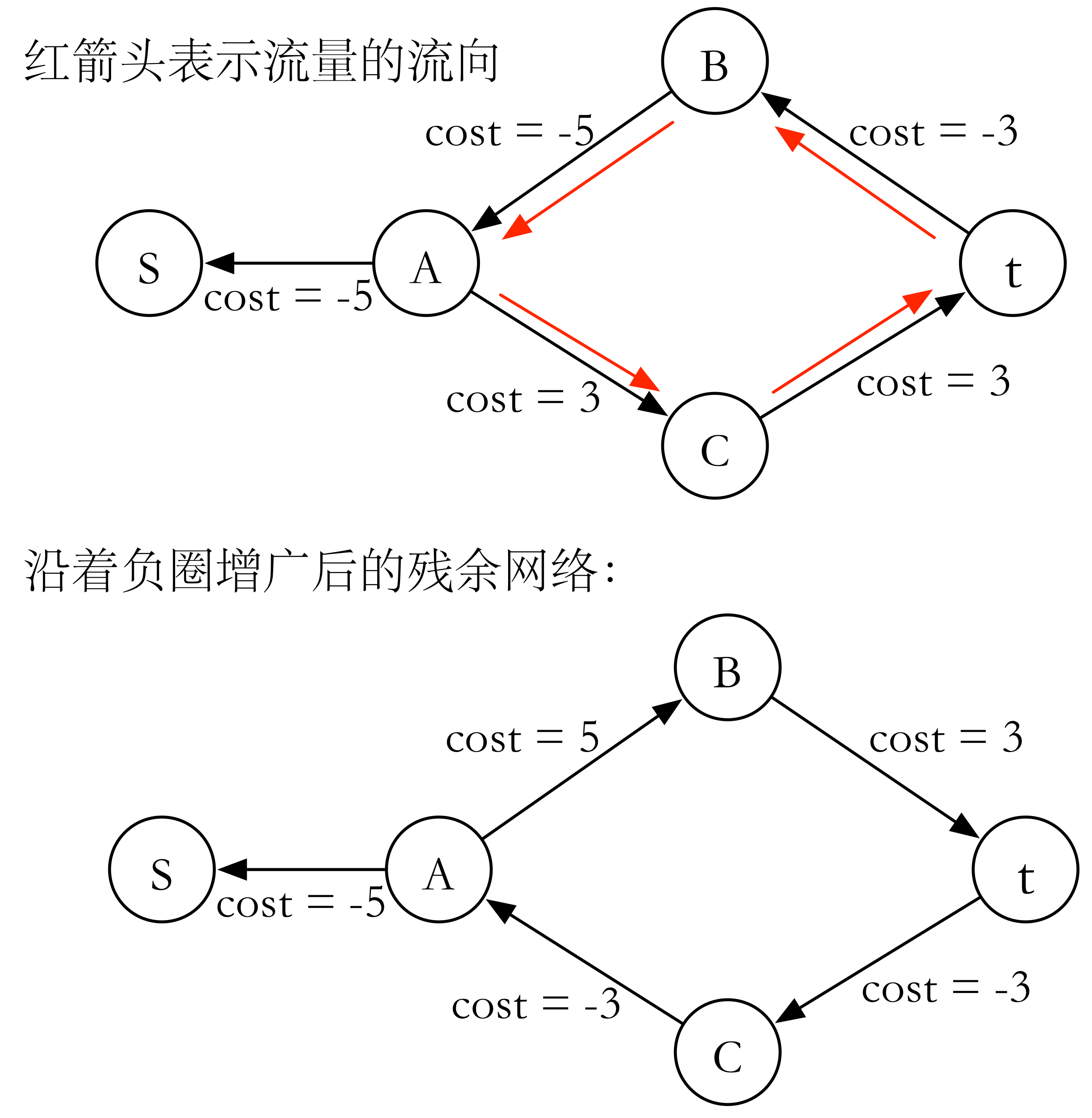
可以看到，沿着负圈增广之后，已经没有负圈存在了，已经达到了当前流量下的最小费用流（也就是最小费用最大流）。所以只要有负圈，就可以增广达到更小费用。

# 应用

求最小费用最大流时，可以先跑出一条可行最大流，然后通过不断消圈调整出最小费用。

更广泛用于残余网络寻找更优解。

# POJ2175 Evacuation Plan

# 题面

原题面很长。

给出已达到最大流的残余网络，求出其是否已达到最小费用，如果未达到则找出更优方案。

# 思路

消圈模板，建出网络后利用 SPFA，如果一个节点被更新了 nn 次则说明图中一定存在负环。题目中没有说必须是最优解，因此只要将负圈上的流量调整 11 即可。

注意一个节点被更新 nn 次不代表其一定在负权圈内。正确做法是从这个节点 vv 开始不断捯它的前驱，如果发现某个节点 uu 被访问了两遍，则说明 uu 一定在负权圈内，再根据 uu 去捯前驱调整负权圈。

# 图解

好像有几个地方标错了 QAQ 凑合看吧

# 代码

#include <stdio.h>
#include <string.h>
#include <queue>
using namespace std;
#define il inline
template <typename T> il T abs(T x) { return x > 0 ? x : -x; }
const int N = 110, M = N * N << 1, INF = 0x3f3f3f3f;
struct coor {
    int x, y, z;
} a[N], b[N];
struct node {
    int u, v, w, f, next;
} e[M];
int h[N << 1], tot = 0;
bool vis[N << 1];
int n, m, s, t;
int cnt[N << 1], pre[N << 1];
il void add(int u, int v, int w, int f) {
    e[tot] = (node) {u, v, w, f, h[u]};
    h[u] = tot++;
}
int bp[N][N], dis[N << 1], p[N][N], occ[N];
deque<int> q;
bool cyc[N << 1];
il void check(int v) {
    
    do {
        cyc[v] = true;
        v = e[pre[v]].u;
    } while(!cyc[v]);
    
    int u = v;
    do {
        --e[pre[v]].w;
        ++e[pre[v]^1].w;
        v = e[pre[v]].u;
    } while(u != v);
                        
    for(int i=1; i<=m; ++i) 
        for(int j = h[n+i]; j != -1; j = e[j].next) 
            if(e[j].v != t) bp[e[j].v][i] = e[j].w;
                                
    printf("SUBOPTIMAL\n");
    for(int i=1; i<=n; ++i) {
        for(int j=1; j<=m; ++j) printf("%d ", bp[i][j]);
        printf("\n");
    }
}
int main() {
    
    scanf("%d%d", &n, &m);
    
    for(int i=1; i<=n; ++i) 
        scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].z);
    
    for(int i=1; i<=m; ++i) 
        scanf("%d%d%d", &b[i].x, &b[i].y, &b[i].z);
    
    for(int i=1; i<=n; ++i)
        for(int j=1; j<=m; ++j)
            scanf("%d", &p[i][j]),
            occ[j] += p[i][j];
    
    memset(h, -1, sizeof h);
    s = 0, t = n+m+1;
    for(int i=1; i<=n; ++i) {
        add(s, i, a[i].z, 0);
        add(i, s, 0, 0); 
    }
    
    for(int i=1; i<=n; ++i) {
        for(int j=1; j<=m; ++j) {
            int f = abs(a[i].x - b[j].x) + abs(a[i].y - b[j].y) + 1;
            add(i, n+j, INF, f);
            add(n+j, i, p[i][j], -f);
        }
    }
    
    for(int i=1; i<=m; ++i) {
        add(n+i, t, b[i].z - occ[i], 0);
        add(t, n+i, occ[i], 0);
    }
    
    memset(dis, 0x3f, sizeof dis);
    
    q.push_front(s);
    vis[s] = true;
    ++cnt[s];
    dis[s] = 0;
    
    while(!q.empty()) {
        int u = q.front();
        q.pop_front();
        vis[u] = false;
        for(int i = h[u]; i != -1; i = e[i].next) {
            int v = e[i].v;
            if(e[i].w and dis[v] > dis[u] + e[i].f) {
                pre[v] = i;
                dis[v] = dis[u] + e[i].f;
                if(!vis[v]) {
                    if(!q.empty() and dis[v] >= dis[q.front()]) q.push_back(v);
                    else q.push_front(v);
                    vis[v] = true;
                    ++cnt[v];
                    if(cnt[v] == t+1) {
                        check(v);
                        return 0;
                    }
                }
            }
        }
    }
    printf("OPTIMAL\n");
    
    return 0;
}
算法证明中的图片引自 Sengxian’s Blog。
  
 更新于